


이전에는 행렬을 곱할때, 그냥 했지만 이번강에서는 이를 체계적으로 다룬다.
다양한 행렬곱셈을 배운 후에, 역행렬(Inverse Matrices)에 대해 다룬다.
행렬 곱하기 를 바라보는 시각은 크게 4가지 방법이 있다.
1. 일반적 방법
2. 행렬 X Column
3. Row X 행렬
4. Column X Row
I . 일반적 방법

C행렬의 C(3,4) 원소가 있다면 이 원소는 어떻게 만들어 졌는가?
==> A의 3번째 row와 B의 4번째 col이 곱해져서 만들어 진다.
이를 수식화 하면
C34 = (row 3 of A) X ( col 4 of B) 가 된다.
일반화 하여 시그마로 있어보이게 쓰면

II . 행렬 X column

C행렬의 col1은 B의 col1이 관여하여 만들어 진 것이다.
이를 명확하게 이해하기 위해 B의 첫번째 행을 고정하고 A의 열들을 1부터 m개 까지 내려보면,
A의 행 하나마다 C의 첫 열의 첫 원소가 되고, 쭉 내리면 열 하나가 만들어 짐을 확인할 수 있다.
길교수 : Columns of C are combinations of columns of A
III . row X 행렬

C의 row1은 A의 row1이 관여하여 만들어 진 것이다.
마찬가지로 명확하게 확인하기 위해 A의 첫 행을 고정하고 B의 열들을 1부터 k까지 이동하며 곱하면,
B의 열 하나마다 C의 첫 행의 첫 원소가 되고, 쭉 이동하면 행 하나가 만들어 짐을 확인할 수 있다.
길교수 : Rows of C are combinations of rows of B
IV . column X row
m by 1 사이즈 열과 1 by p사이즈 의 행을 곱하면 m by p 사이즈의 행렬이 나온다.
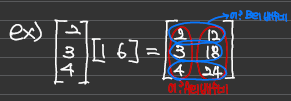
A(m by n) 와 B(n by p)를 곱한 결과는 A의 열과 B의 행을 n번곱해 이를 모두 더한 값과 같다.
이를 수식으로 쓰면

Block Multiplication

행렬이 클때 블록으로 나눠 곱할 수 있다.
AB=C라 했을때 C의 1행 1열의 원소는 A1B1+ A2B3로 나타낼 수 있다.
(강의에서는 Square Matrix라고 가정하는 것 같다)
Inverse Matrix ( square matrix의 경우)
Inverse matrix는 이전에 설명했듯 Identity matrix를 만들어 주는 행렬이다.
역행렬이 존재하는 행렬을 invertible, non-singular 하다고 한다.
A의 역행렬은 \[A^{-1}\]로 표현한다.
왼쪽과 오른쪽에 곱해 Identity matrix를 만들수 있으므로
\[A^{-1}A = I= A*A^{-1}\]
으로 나타낼 수 있다.
그렇다면 Singular은 역행렬이 존재하지 않는 경우인데, 예를 보자.

이 행렬의 경우 어떤 행렬을 곱하면 행이든 열이든 배수 관계가 성립하여 identity가 될 수 없다.
즉, column들의 조합이 한 직선에 놓여 있다.
역행렬을 가지는지 아닌지 행렬식(determinent)를 이용하여 구할 수 있는데 이는 강의 중반에 나온다.
역행렬을 가지는지 확인하는 다른 방법은 Ax=0을 만족하는 x를 찾을 수 있는지 없는지 찾아 알 수 있다.
won't have inverse = can't find a vector with Ax = 0
예를 들어 위 A의 경우
\[\begin{bmatrix} 1 & 3\\ 2 & 6 \end{bmatrix} \begin{bmatrix} -3\\ 1 \end{bmatrix} = \begin{bmatrix} 0\\0 \end{bmatrix}\]
가 성립하므로 역행렬을 가지지 않는다.
그 이유는 다음과 같다.

A에서 2행 2열이 7로 바뀐 행열을 가정해 보자.

이렇게 되면 2개의 Linear System을 풀어야 한다..
이때 Gauss-Jordan 소거법을 이용하여 2개의 sysytem을 한번에 구할 수 있다.

Augmented Matrix에서 왼쪽행렬을 Identity matrix가 되게 소거를 하면
오른쪽 행렬에 Inverse Matrix가 된다.
\[E_{n}\cdot \cdot \cdot E_{2}E_{1}A = I\]
에서 A왼쪽에 E행렬들을 곱한 것들을 E라 했을때,
E[ A | I ] => [ I | E ]
EA=I로 나타낼 수 있다. E는 A의 역행렬이다.
'Linear Algebra' 카테고리의 다른 글
| Linear Algebra(18.06) - 5.Transpose, Permutation, Space R^n (0) | 2021.06.07 |
|---|---|
| Linear Algebra(18.06) - 4. Factorization into A=LU (0) | 2021.05.01 |
| Linear Algebra(18.06) - 2.Elimination with matrices (0) | 2021.03.18 |
| Linear Algebra(18.06) - 1. Geometry of Linear Equation (0) | 2021.03.05 |
| Linear Algebra 책 리뷰, 강의(MIT 18.06) (0) | 2021.03.01 |