


그동안 행렬관련해서 기초적인 지식이나 연산들에 대해 배웠다.
선형대수를 제대로 시작하는 부분은 벡터공간을 이해하는 것 부터라고 하신다.

일단 Permutation Matrix P는 행렬에 곱했을때, 행을 바꿔주는 행렬이다.
행을 바꾸는 경우는 A=LU분해를 할때, 행을 바꿔야 Pivot을 찾을 수 있는 경우였다.

행 교환이 없다면 바로 A=LU를 구할 수 있는데, 필요하다면 P를 곱한 PA를 기준으로 분해를 하면 된다.

배운 내용이지만 P의 역행렬은 P의 전치행렬이다. 따라서 P^T P = I가 된다.

I를 통해 만들 수 있는 P의 개수는 n!개 이다.
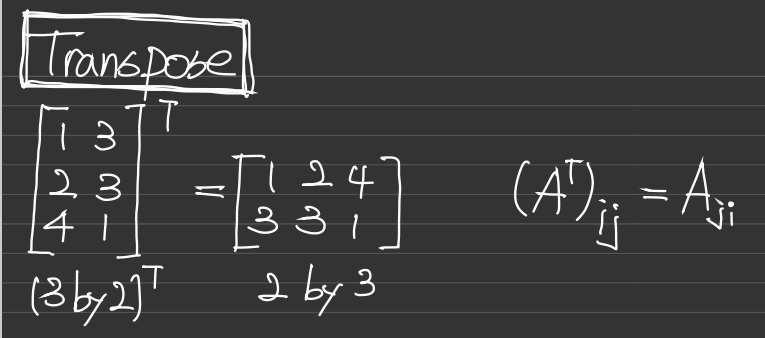
전치행렬(Transpose Matrix)는 행과 열이 바뀐 행렬을 말한다.

대칭행렬(Symmetric Matrix)는 대각선을 기준으로 대칭인 행렬을 말한다.
즉, 전치를 해도 그대로인 행렬을 말한다. (i행 j열의 원소 == j행 i열의 원소인 경우)


Rectangular(n by n 아닌경우)는 대칭일 수가 없다. 하지만 R과 R^T를 곱하면 대칭이다(순서상관 X)

R^TT=R이기 때문이다.
다음주제인 벡터공간으로 넘어간다.

벡터공간의 핵심은 벡터들을 더할수 있고, 곱할 수 있어야 한다는 점이다.
앞의 내용에서 선형 결합을 배웠는데, 선형결합이 벡터공간의 규칙을 따른다고 보면 된다.

예를 들어 2차원 공간을 예로 들 수 있다. 2차원 공간 안에 있는 벡터들을 더하거나 스칼라 값을 곱해도 계속 2차원평면 안에 있기 떄문이다.

벡터공간의 중요한 특징 중 하나인데, 스칼라 값중 0도 곱할 수 있어야 한다.

마찬가지로 3차원공간도 더하거나 빼는 것이 3차원 안에 있기 때문에 벡터공간이고,
n차원 공간으로도 확장시켜 이를 적용해 볼 수있다.

2차원 공간중 1사분면만을 보고 벡터공간인지 따져본다.
1사분면안에 있는 벡터들을 더하면 계속 1사분면 안에 있다.
다음은 곱하는 문제인데, 양수인 경우에는 안에 있지만 음수를 곱하게 되면 3사분면에 위치하게 된다.
(덧셈은 닫혀있지만 곱셈은 닫혀있지 않는다고 표현한다.)
(Closed under addition not under multiplication)
그러면 1,3사분면은 벡터공간인가? 라는 의문이 들 수 있다
1사분면에 있는 벡터와 3사분면에 있는 벡터를 더하면 2사분면에 위치하므로 벡터공간이 아니다.
(not closed under addition)
덧셈과 곱셈에 대해서 닫혀야 하므로 벡터공간은 선형결합에 닫혀있다고 표현할 수도 있다.
(Closed under linear combination)
벡터공간 안에 또 다른 벡터공간을 부분공간(Subspace)이라고 부른다

예를 들어 임의의 벡터 v를 통해 cv의 집합을 보자, 이는 직선이 나올 것이고,
곱셈에 나온 직선이므로 곱셈에 대해 닫혀있을 것이다. 직선중 두 벡터를 임의로 더하여도 직선안에 있으므로
이는 부분공간의 예라고 할 수 있다.
하지만 직선이라고 모두 부분공간인 것은 아니다. 원점을 지나지 않는 직선을 볼때,
곱셈에 대해 닫혀있으려면 0을 곱했을때도 직선 안에 있어야 하는데, 원점을 지나지 않으므로 부분공간이 아니다.

R^2의 부분공간들이다.

3차원 공간일 떄는 직선뿐만아니라 3차원 공간 안에 평면도 부분공간이다.

column들을 선형결합해서 얻는 공간을 Column Space(C(A))라고 한다

3차원 공간안에서 독립한 두 column들을 선형결합하면 평면이 만들어지는데 이 평면은 R^3의 부분공간이다.
'Linear Algebra' 카테고리의 다른 글
| Linear Algebra(18.06) - 4. Factorization into A=LU (0) | 2021.05.01 |
|---|---|
| Linear Algebra(18.06) - 3.Multiplication and Inverse Matrices (0) | 2021.04.05 |
| Linear Algebra(18.06) - 2.Elimination with matrices (0) | 2021.03.18 |
| Linear Algebra(18.06) - 1. Geometry of Linear Equation (0) | 2021.03.05 |
| Linear Algebra 책 리뷰, 강의(MIT 18.06) (0) | 2021.03.01 |