1강은 연립방정식으로 시작한다.

연립방정식은 n개의 식과 n개의 미지수가 주어지면 해를 구할 수 있다.
해는 유일할 수도있고 그렇지 않을 수도 있음.
연립방정식을 3가지 관점에서 바라본다.
1. Row Picture
방정식을 함수로 나타내고 두 함수가 점이 (미지수가 2개인 연립방정식은 점) 해 이다.
2. Column Picture (길교수피셜 중요)
벡터들의 합으로 해를 만족하는 벡터를 구할 수 있음.
3. Matrix Picture
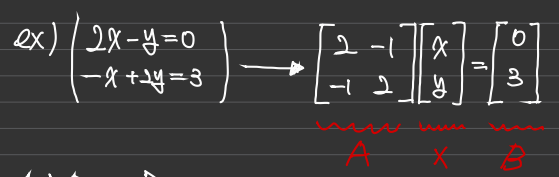
왼쪽 방정식을 오른쪽처럼 AX=b로 쓸수 있는데 A를 coefficient matrix라고 한다.(계수를 나타내는 행렬 이라는 뜻)
강의가 진행되면 A가 특수한 상황이 아닌경우 역행렬 이라는 것을 구한 다음 좌변 우변에 곱해 x를 구할수 있다.
위의 예시를 통해 살펴본다.
1) Row Picture
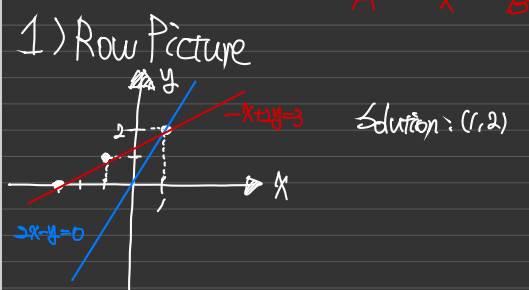
중,고등학교때 배운 방식. 두 식을 방정식으로 그린 후 만나는 점을 확인한다.
Row 1,2는 각각 [2 -1], [-1 2]인데 두 직선의 각 x, y계수를 나타냄
2) Colum Picture

위에 A로 나타낸 행렬을 column으로 끊어서 각각 col1,col2로 한다.(Ax=b에서 Ax를 유심히 관찰)
Ax는 x * col1 + y * col2로 나타낼 수 있다. (이를 선형 결합-Linear Combination이라고 한다)
col1,2를 벡터로 나타내면 오른쪽의 그림과 같다. col1과 col2를 적절하게 섞어 [0 ; 3]을 나타내야 한다.(;는 행 구분 표시)
고등학교때 벡터의 합을 배웠는데 평행사변형 방법과 이동시키고 삼각형으로 더하는 방법이 있었는데
col1에 col2를 두번 더하면 이를 벡터의 합으로 표시했을때 col1의 시작점에서 col2를 두번 더한 것의 끝점을 연결한 벡터가 나온다. 그리고 이는 [0 ; 3]이고 방정식의 해는 col1을 1번(=x) col2를 2번(=y) 더한 것이므로 (1,2)가 해이다.
3차원 예시

마찬가지로 Ax=b로 나타낼 수 있다.
1) Row Picture

아까는 직선이였을 뿐 차원만 늘어났고 다른게 없다.
세 평면이 모두 만나는 점이 해이다(특수한 경우 점이 아닐 수 있음)
2 ) Column Picture

마찬가지로 각 Column들에 대해 선형결합을 한 후, 3차원 공간에 벡터로 표현한다.
해는 딱 보면 (0,0,1)이라는 사실을 알 수 있다.
만약 [0 ; -1 ; 4]를 구하는 문제라면?? (빨간색 표시)
col1과 col2를 더해주면 해가 되므로 이 경우에는 (1,1,0)이다.

3차원 공간의 모든 점b에 대해서 Ax=b를 만족하냐는 뜻은 위의 세개의 column들이 3차원 공간을 다 채우는가?
라는 질문과 같은 뜻이다. 위의 column들로 보면 답은 "예"이다.
이럴때 column들이 독립되어 있다고 말하며, 이 행렬을 Non-Singular Matrix, Invertible Matrix라고 한다.
반대 개념은 Singular Matrix, Not-Invertible Maxtrix이다.

그렇다면 언제 3차원 공간을 못채울까?
3개의 column들이 독립이 아닐때 그렇다.

3차원 공간을 예로 들자면 col1, col2, goal벡터를 이용하여 3차원을 채우고 싶은데
goal벡터 대신 col1과 col2가 결합한 벡터가 있을 경우 세 벡터가 한 평면에 갖힌다.
위에서 말 했던 것처럼 이 행렬을 Singular, Not Invertible 행렬이라고 한다.
ex) 3차원 구성하는 단위벡터는 (1,0,0) (0,1,0) (0,0,1)인데
셋중 하나가 한 벡터의 배수이거나 나머지 두 벡터의 합이면 평면에 갖힌다.(직접 해보면 보임)
후에 판별식(Determinent)라는 개념을 배우면 Singular인지 Non-Singular인지 판별할 수 있게 된다.

마지막은 행렬 곱셈의 두가지 방법이다.
위는 Row Pic방식, 아래는 Col Pic방식이다.
위의 방식은 고등학교나 대학교때 행렬 곱셈을 배울때 기본적으로 쓰는 방법이고,
아래의 방식은 선형대수시간에 처음 배운 방법 같은데 길버트 교수님이 좋아하는 방식이고 중요한 개념이라 하셨다.
'Linear Algebra' 카테고리의 다른 글
| Linear Algebra(18.06) - 5.Transpose, Permutation, Space R^n (0) | 2021.06.07 |
|---|---|
| Linear Algebra(18.06) - 4. Factorization into A=LU (0) | 2021.05.01 |
| Linear Algebra(18.06) - 3.Multiplication and Inverse Matrices (0) | 2021.04.05 |
| Linear Algebra(18.06) - 2.Elimination with matrices (0) | 2021.03.18 |
| Linear Algebra 책 리뷰, 강의(MIT 18.06) (0) | 2021.03.01 |